Physically based shading and image based lighting(翻译)
请尊重原作者的工作,转载时请务必注明转载自:www.xionggf.com
Light is complicated, and we really don’t have a full equation that accurately models light in the real world. This might sound confusing because of all the recent strides in CG and visual technology. Well, it’s all approximate – it’s just that we select functions which approximate really well. The unfortunate truth is: There is no one equation for light – only approximations.
光线很复杂,我们真的没有一个完整的方程式可以准确地模拟现实世界中的光线。 由于CG和视觉技术的最新发展,这听起来可能令人困惑。好吧,这都是近似的-只是我们选择了非常近似的函数。 不幸的事实是:没有一个完全模拟现实世界的光方程,只有一个近似的版本。
Blinn-Phong is an approximation. If you’ve been following my recent blog posts you might have identified that the lighting model I have been using since the start has been Blinn-Phong. But let’s face it, Blinn-Phong hasn’t really improved with age – the paper on this algorithm was published originally in 1977. At the time of writing, it’s almost a 40 year-old approximation for lighting. Can’t we do better?
Blinn-Phong 是一个近似模型。如果您一直在关注我最近的博客文章,则可能已经确定。自开始以来我一直在使用的照明模型是Blinn-Phong。但是请面对现实,Blinn-Phong并没有随着岁月的流逝而真正提高-有关此算法的论文最初发表于1977年。在撰写本文时,对光照模拟的近似值被使用了已接近40年。难道我们没有更好的模拟,使得效果更为逼真吗?
Physically Based Shading

Modern shading models are often referred to as Physically Based. They feature a more complicated lighting model, which separates into multiple equations with three special interchangeable factors – the whole equation forms a Bidirectional Reflectance Distribution Function (BRDF) known as the Cook-Torrance Model. A BRDF is essentially a function which models the amount of reflected light across the surface of an object. Bidirectional means that if the light and the view were to switch places, the equation would produce the same results. Reflectance is just what it sounds like, some factor representing the amount of light reflected. Distribution is the integral of the probability, in our case the distribution is the light over the object. Much like cumulative distribution functions in probability, we expect that the sum of all it’s parts to equal 1 (conservation of energy, in our case). And Function – it is a function. :) The Cook-Torrance Model can be expressed as follows:
现代的 着色模型(shading model) 通常称为“基于物理”。它们具有更复杂的照明模型,该模型可通过三个特殊的可互换因子分解成多个方程式-整个方程式形成了 双向反射分布函数(BRDF) ,称为 Cook-Torrance 模型。BRDF本质上是一种对物体表面反射的光量进行建模的功能。 双向表示,如果灯光和视图切换位置,则该方程将产生相同的结果 。反射率 就是听起来的样子,某些系数代表反射的光量。分布是概率的整数,在我们的例子中,分布是照射在物体表面上的光。与概率的累积分布函数非常相似,我们希望所有部分的总和等于1(在我们的示例中为能量守恒)。 功能-它是一种功能。 :) Cook-Torrance模型可以表示为:
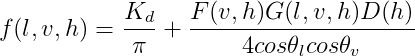
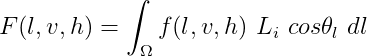
This model represents the amount of light reflected from an object (similar to Blinn-Phong) but with an approximation that takes into account the microscopic levels of detail on the surface of the object. The three functions F, G, and D are the specular factors which represent (respectively) Fresnel, Geometric Occlusion, and Normal (of Microfacet) Distribution. The power of this kind of BRDF is that different specular functions can be swapped out with whatever approximation you see fit (so long as they correspond to the same geometric meaning). What I mean by this is that there are several approximations to each of these functions, you only need to choose one, but you have the freedom to select whichever you want.Let’s discuss the factors in more detail.
该模型表示从物体反射出来的光量是多少(类似于Blinn-Phong),但此模型考虑了物体表面的微观细节水平。F,G和D这三个函数是用于描述镜面反射部分的系数,分别代表 菲涅耳 , 遮挡-蒙盖 和 微表面法线的正态分布 。这种BRDF的功能在于,可以使用您认为合适的任何近似(只要它们对应于相同的几何含义)函数,即前面的F,G和D这三个函数,去组合实现不同的镜面反射效果。我的意思是,每个功能都有多个近似值,您只需要选择一个即可,但是您可以自由选择所需的任何一个。让我们更详细地讨论这些因素。
Fresnel Factor


上图是完全打开fresnel的效果,右图是完全关闭fresnel的效果
Fresnel is the amount of light that reflects based on the current angle of incident between the light and the normal. As the incident angle becomes increasingly large, the amount of light that reflects into our eyes becomes greater. At 90° Angle of Incidence (AOI) the amount of light that reflects is 100%. An interesting fact about the Fresnel factor is that every type of known material has reflection – yes, even the ones you wouldn’t expect. If you look towards a light where you and the light have an increasing angle of incidence, you can force out this specular factor. It would make sense that no object completely consumes light, that wouldn’t physically make sense.
菲涅耳是根据光和法线之间的当前入射角,计算出反射的光量。随着入射角变得越来越大,反射到我们眼睛中的光量也会越来越大。 在 90°入射角(Angle of Incidence AOI) 下,反射的光量为 100% 。关于菲涅耳系数的一个有趣事实是,每种已知的材质都有反射-是的,甚至是您不希望看到的。如果朝着入射光角度不断增大的方向看,(译注:这句话的意思是说,如果你沿着法线的方向,视线垂直地看向被观察物,则这时候基本上看不到任何的高光反射,而如果视线和法线基本垂直的话。高光反射就变得很强烈)则可以排除此镜面反射因子。没有物体完全消耗光是有道理的,从物理上讲是没有道理的。
