An Introduction to shader derivative functions（翻译）

请尊重原作者的工作，转载时请务必注明转载自：www.xionggf.com

原文地址

Partial difference derivative functions (ddx and ddy in HLSL[a], dFdx and dFdy in GLSL[b]) (in the rest of this article I will use both terms according to the code examples I will provide) are fragment shader instructions wich can be used to compute the rate of variation of any value with respect to the screen-space coordinates.

偏导数函数（在HLSL中为ddx和ddy，GLSL中为dFdx和dFdy）。在本文的其余部分中，我将根据我将提供的代码示例使用这两个术语）都是可以使用的片元着色器指令，可用于计算任何数值相对于 屏幕空间坐标 的变化率。

Derivatives computation

During triangles rasterization, GPUs run many instances of a fragment shader at a time organizing them in blocks of 2×2 pixels. Derivatives are calculated by taking differences between the pixel values in a block; dFdx subtracts the values of the pixels on the left side of the block from the values on the right side, and dFdy subtracts the values of the bottom pixels from the top ones. See the image below where the grid represents the rendered screen pixels and dFdx, dFdy expressions are provided for the generic value p evaluated by the fragment shader instance at (x, y) screen coordinates and belonging to the 2×2 block highlighted in red.

在对三角形进行光栅化期间，GPU一次针对2x2个像素执行片元着色器。通过获取着2x2个像素块中像素值之间的差异，来计算导数：dFdx从右侧的值中减去块左侧的像素值，而dFdy从顶部的像素中减去底部像素的值。请参见下图，其中的网格表示渲染的屏幕像素，并且dFdx，dFdy函数在片元着色器中，对在（x，y）屏幕坐标处的片元，根据函数p(x,y)，求解了此片元的导数值，该值对应于红色突出显示的2×2块。

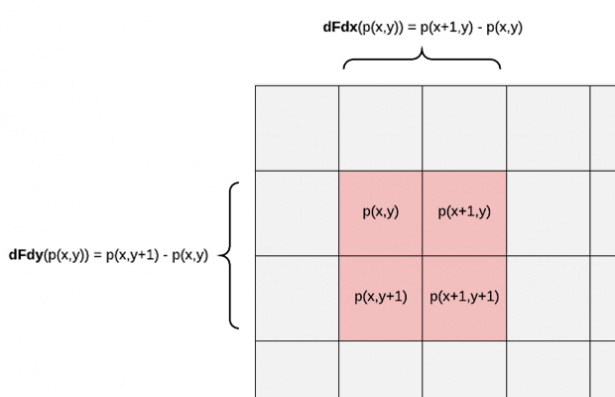
Derivatives can be evaluated for every variable in a fragment shader. For vector and matrix types, derivatives are computed element-wise.

可以为片元着色器中的每个变量求导数。对于矢量和矩阵类型，导数是逐元素计算的。

Derivatives functions are fundamental for texture mipmaps implementation and are very useful in a series of algorithms and effects, in particular when there is some kind of dependence on screen space coordinates (for example when rendering wireframe edges with uniform screen pixel thickness).

导数函数是纹理mipmap实施的基础，并且在一系列算法和效果中非常有用，尤其是在某种程度上依赖于屏幕空间坐标时（例如，以均匀的屏幕像素厚度渲染线框边缘时）。

Derivatives and mipmaps

Mipmaps are pre-computed sequences of images obtained by filtering down a texture into smaller sizes (each mipmap level is two times smaller than the previous). They are used to avoid aliasing artifacts when minifying a texture.

Mipmap是通过将纹理过滤成更小的尺寸（每个mipmap级别比前一个小两倍）而获得的预先计算的图像序列。 它们用于在最小化纹理时避免 反褶假影（aliasing artifacts） 。

Mipmapping is also important for texture cache coherence, since it enforces a near-one texel to pixel ratio: when traversing a triangle, each new pixel represents a step in texture space of one texel at most. Mipmapping is one of the few cases in rendering where a technique improves both visuals and performance.

Mipmapping对于纹理缓存的一致性也很重要，因为它强制实现接近1的像素与像素的比率：遍历三角形时，每个新像素最多代表一个纹素在纹理空间中的步进。Mipmapping是为数不多的能同时改善视觉效果和性能的渲染技术的一种。

Derivatives are used during texture sampling to select the best mipmap level. The rate of variation of the texture coordinates with respect to the screen coordinates is used to choose a mipmap; the larger the derivatives, the greater the mipmap level (and the lesser the mipmap size).

在纹理采样期间使用导数来选择最佳的Mipmap级别。根据 纹理坐标相对于屏幕坐标的变化率 来选择mipmap。 导数越大，mipmap级别越大（并且mipmap大小越小） 。

Face normal computation (flat shader)

Derivatives can be used to compute the current triangle’s face normal in a fragment shader. The horizontal and vertical derivatives of the current fragment’s world-position are two vectors laying in the triangle’s surface. Their cross product is a vector orthogonal to the surface and its norm is the triangle’s normal vector (see the 3d model below). Particular attention must be paid to the ordering of the cross product: being the OpenGL coordinate system left-handed (at least when working in window space which is the context where the fragment shader works) and being the horizontal derivative vector always oriented right and the vertical down, the ordering of the cross product to obtain a normal vector oriented toward the camera is horizontal x vertical (more about cross products and basis orientations in this article). The interactive model below shows the link between screen pixels and fragmets over a triangle surface being rasterized, the derivative vectors on the surface (in red and green), and the normal vector (in blue) obtained by the cross product of the twos.

导数可用于在片元着色器中计算当前三角形的面法线。当前片元的在世界坐标系位置点所对应的水平方向偏导数和垂直方向偏导数，是放置在三角形表面中的两个向量。它们的叉积是正交于曲面的向量，其 单位化值（norm） 是三角形的法线向量（请参见下面的3d模型）。必须特别注意叉积计算时所遵循的顺序法则：如果在OpenGL环境下，用左手法则。通过叉积计算，获得朝向相机的法向矢量。这叉积的顺序为 水平向量 x 垂直向量 （本文中有关叉积和基本方向的更多信息）。下面的交互式模型显示了在光栅化的三角形表面上的屏幕像素和片元之间的关联，该表面上的导数矢量（红色和绿色）以及通过两者的叉积获得的法线矢量（蓝色）。

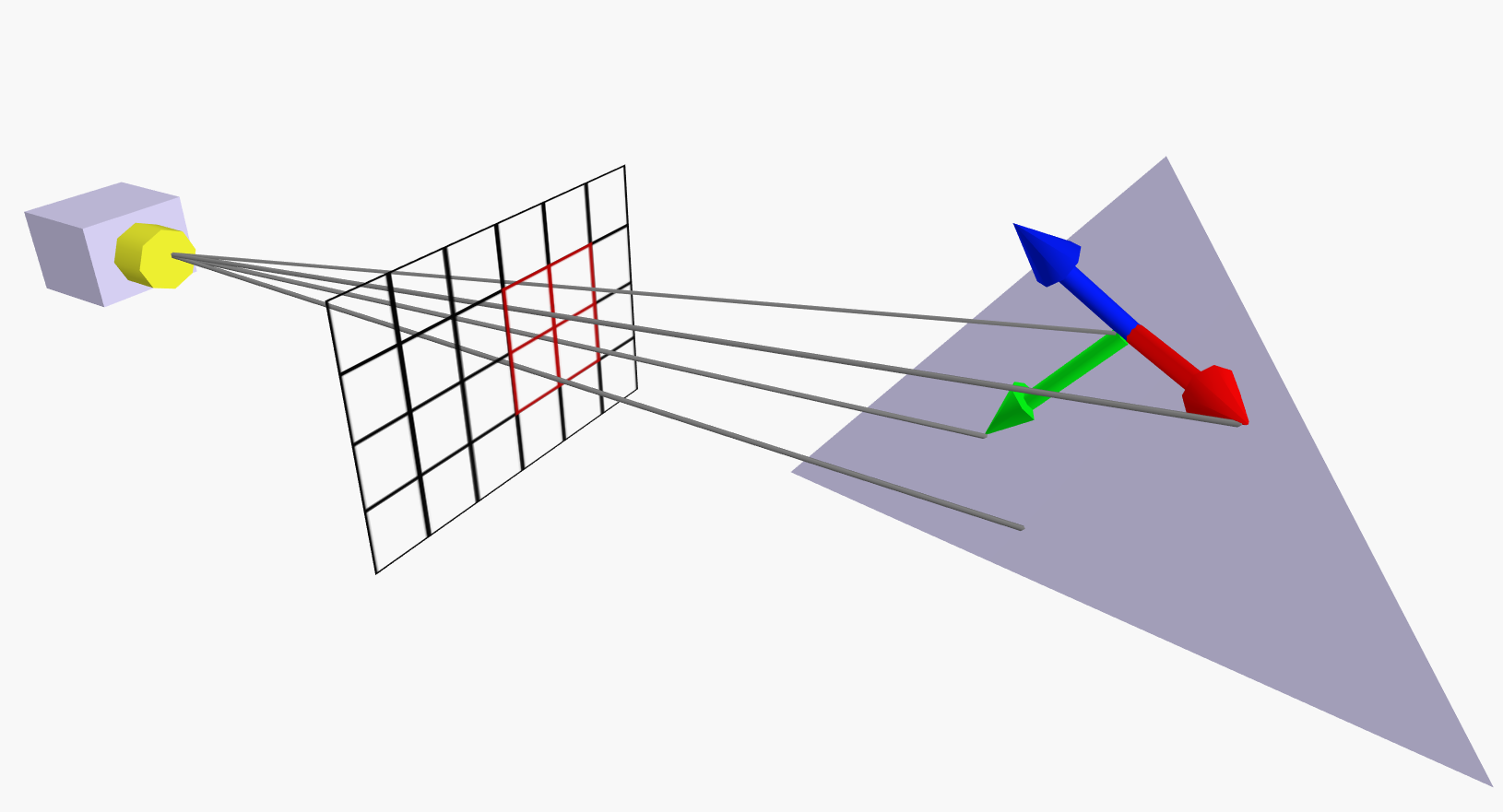
Here is a GLSL code line to compute a flat normal given the fragment position pos in camera space:

下面是一条GLSL代码行，给定相机空间中的片段位置pos，用于计算平面法线

normalize( cross(dFdx(pos), dFdy(pos)) );

And below there is a complete pocket.gl demo with a vertex and fragment shader at work on an Utah Teapot. You can toggle the flat shader using the Flat shaded checkbox.

下面是一个完整的演示，其中包含用来渲染一个 犹他茶壶 顶点着色器和片元着色器。您可以使用“flat shader”复选框在 平面着色器 和 平滑着色器 模式之间切换。

下面两图分别是smooth模式和flat模式的渲染效果：

下面的是顶点着色器

varying vec3 normalInterp;
varying vec3 pos;

void main(){
    gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
    vec4 pos4 = modelViewMatrix * vec4(position, 1.0);

    normalInterp = normalMatrix * normal;
    pos = vec3(pos4) / pos4.w;
}

下面的是片元着色器

precision mediump float;

varying vec3 pos;
varying vec3 normalInterp;

uniform float bFlat; // 用来切换flat shader和smooth shader模式的变量

const vec3 lightPos     = vec3(200,60,100);
const vec3 ambientColor = vec3(0.2, 0.0, 0.0);
const vec3 diffuseColor = vec3(0.5, 0.0, 0.0);
const vec3 specColor    = vec3(1.0, 1.0, 1.0);

void main() {
    vec3 normal = mix(normalize(normalInterp), 
        normalize(cross(dFdx(pos), dFdy(pos))), bFlat);
    vec3 lightDir = normalize(lightPos - pos);

    float lambertian = max(dot(lightDir,normal), 0.0);
    float specular = 0.0;

    if(lambertian > 0.0) {
        vec3 viewDir = normalize(-pos);
        vec3 halfDir = normalize(lightDir + viewDir);
        float specAngle = max(dot(halfDir, normal), 0.0);
        specular = pow(specAngle, 16.0);
    }

    gl_FragColor = vec4(ambientColor + 
    lambertian * diffuseColor + specular * specColor, 1.0);
}

Derivatives and branches

Derivatives computation is based on the parallel execution on the GPU’s hardware of multiple instances of a shader. Scalar operations are executed with a SIMD (Single Instruction Multiple Data) architecture on registers containing a vector of 4 values for a block of 2×2 pixels. This means that at every step of execution, the shader instances belonging to each 2×2 block are synchronized making derivative computation fast and easy to implement in hardware, being a simple subtraction of values contained in the same register.

导数计算基于在GPU硬件上的并行执行多个着色器程序实例。 标量操作使用SIMD（单指令多数据）架构，在包含2×2像素块共4个值向量的寄存器上执行。 这意味着在执行的每个步骤中，属于每个2×2块的着色器实例都是同步的，从而使派生计算快速且易于在硬件中实现，只需对包含在同一寄存器中的值进行简单的减法即可。

But what happens in the case of a conditional branch? In this case, if not all of the threads in a core take the same branch, there is a divergence in the code execution. In the image below an example of divergence is shown: a conditional branch execution in a GPU core with 8 shader instances. Three instances take the first branch (yellow). During the yellow branch execution the other 5 instances are inactive (an execution bitmask is used to activate/deactivate execution). After the yellow branch, the execution mask is inverted and the blue branch is executed by the remaining 5 instances.

但是在条件分支的情况下会发生什么呢？在这种情况下，如果不是内核中的所有线程都采用相同的分支，则代码执行会有分歧。在下面的图像中显示了一个 差异(divergence) 示例：具有8个着色器实例的GPU内核中的条件分支执行。三个实例采用第一个分支（黄色）。在执行黄色分支期间，其他5个实例处于非活动状态（执行位掩码用于激活/取消激活执行）。 在黄色分支之后，执行掩码将反转，剩余的5个实例将执行蓝色分支。

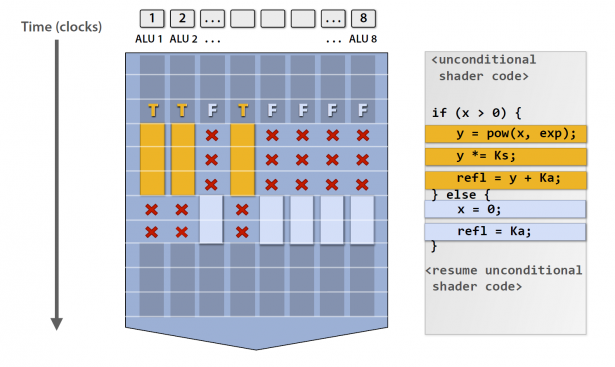
In addition to the efficiency and performance loss of the branch, the divergence is breaking the synchronization between the pixels in a block making derivatives operations undefined. This is a problem for texture sampling which needs derivatives for mipmap level selection, anisotropic filtering, etc. When facing such a problem, a shader compiler could flatten the branch (thus avoiding it) or try to rearrange the code moving texture reads outside of the branch control flow. This problem can be avoided by using explicit derivatives or mipmap level when sampling a texture.

除了分支的效率和性能损失外，差异还破坏了一个块中像素之间的同步，从而导致派生运算不确定。 这是纹理采样的一个问题，需要用于mipmap级别选择， 各向异性过滤（anisotropic filtering） 等的导数。 遇到此类问题时，着色器编译器可能会使分支 变平(flatten) （因此避免了使用分支），或者尝试将代码移动纹理读取的代码重新排列在分支控制流之外。 采样纹理时，可以通过使用显式导数或mipmap级别来避免此问题。

Below you can see a HLSL branching experiment written in UE4 using a custom expression node.

在下面，您可以看到使用自定义表达式节点以UE4编写的HLSL分支实验。

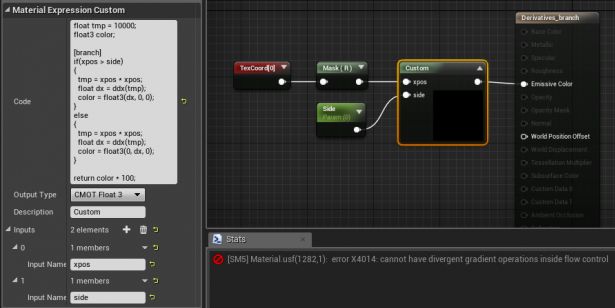
Here is the shader code I’m using in the previous example:

这是我在上一个示例中使用的着色器代码：

float tmp = 10000;
float3 color;

[branch]
if(xpos > side)
{
    tmp = xpos * xpos;
    float dx = ddx(tmp);
    color = float3(dx, 0, 0);
}
else
{
    tmp = xpos * xpos;
    float dx = ddx(tmp);
    color = float3(0, dx, 0);
}

return color * 100;

The purpose of this experiment is to see what happens when derivatives are used inside a divergent block. Suppose that the code above be executed on a GPU core. When a subset of the pixels in a block enters the first branch, the value of tmp for the inactive pixels waiting for the second branch execution should be still 10000. So the ddx function should give a spike for some pixels on divergent blocks. Note the [branch] attribute before the if to force branching using control flow instructions.

该实验的目的是查看在 离散块（divergent block） 中使用导数时会发生什么。 假设以上代码在GPU内核上执行。当块中像素的子集进入第一分支时，等待第二个分支执行的非活动像素的tmp值仍应为10000。因此ddx函数应为发散块上的某些像素提供尖峰。 注意，如果要使用控制流指令强制分支，请注意[branch]属性。

As you can see in the picture above, the compiler gives the following error for that piece of code: “cannot have divergent gradient operations inside flow control“, but when the [branch] attribute is removed, the code compiles fine but no spikes are visible during rendering, meaning that the branch has been flattened.

如您在上图中所看到的，编译器对该代码段给出了以下错误：“在流控制内不能有不同的梯度运算”，但是当删除[branch]属性时，代码可以正常编译，但不会出现尖峰。在渲染过程中可见，表示分支已被展平。

Revealing the block aligning of derivatives

Here is a simple experiment that reveals the inner block alignment of shader derivatives. Look at the following pocket.gl sandbox.

这是一个简单的实验，揭示了着色器导数的内部块对齐。下面是着色器代码：

uniform vec2 resolution;

uniform float odd_step;
uniform float show_derivative;

void main() {
    // center_x is at center x snapped to the nearest even position
    float center_x = floor(resolution.x / 4.0) * 2.0;

    // snap center_x to an odd number if odd_step is 1
    center_x += odd_step;
    
    // Step function is 0 when p.x < step_pos, 1 when p.x >= step_pos
    float step = ceil(clamp((gl_FragCoord.x - center_x) / resolution.x, 0.0, 1.0));

    // The alpha variable is used to select one of two colors
    float alpha = show_derivative == 1.0 ? dFdx(step) : step;

    vec3 color = mix(vec3(0.96, 0.96, 0.68), vec3(0.68, 0.1, 0.1), alpha);

    gl_FragColor = vec4(color, 1.0);
}

The above shader implements a step function over the x axis. We want to compute its derivative. The derivative of a step function would be a Dirac delta function in the continuous domain, but in the shader’s discrete domain the delta function will be equal to 1 when the step jumps from 0 to 1, and 0 elsewhere. Select the Show Derivative checkbox and toggle the Step on odd pix checkbox to snap the Step position to an even (unchecked) or an odd (checked) pixel at the center of the viewport; you’ll see how dFdx(step) changes when moving the transition point from an even to an odd pixel.

上面的着色器在x轴上实现了步进功能。我们要计算其导数。阶跃函数的导数在连续域中是Dirac增量函数，但是在着色器的离散域中，当阶跃从0跳到1时，delta函数将等于1，而在其他地方则为0。选中“显示微分”复选框，并选中“在奇数像素上移动”复选框，以将“位置”捕捉到视口中心的偶数（未选中）或奇数（选中）像素；您会看到将过渡点从偶数像素更改为奇数像素时dFdx（步进）的变化。

Because the derivative computation is performed over blocks of 2×2 pixels, we should expect two different results depending on where the step transition occurs:

由于微分计算是在2×2像素的块上执行的，因此根据阶跃转换发生的位置，我们应该期望得到两个不同的结果：

• Case 1. If the step transition falls in the middle of a 2×2 block of pixels, we’ll see a vertical line with 2 pixel thickness (the derivative is equal to 1 for each pixel in the 2×2 block, hence the 2 pixel thickness). This happens when the step falls on an odd pixel.
• Case 2. The step transition falls in the middle of two neighbouring 2×2 blocks of pixels. In this case we won’t see any vertical line because both the blocks will compute a derivative equal to 0. This happens when the step falls on an even pixel.

• 情况1：如果阶跃过渡位于2×2像素块的中间，我们将看到一条垂直线，具有2个像素的厚度（对于2×2块中的每个像素，导数等于1，因此2像素厚度）当台阶落在奇数像素上时会发生这种情况。
• 情况2：阶跃过渡落在两个相邻的2×2像素块的中间。在这种情况下，我们看不到任何垂直线，因为两个块都将计算出等于0的导数。这种情况发生在台阶落在偶数像素上时。

As an exercise, try to modify the shader code of the above sandbox in order to show an horizontal step function and an horizontal derivative line.

作为练习，请尝试修改上述沙箱的着色器代码，以显示水平阶跃函数和水平导数线。

These aliasing artifacts are caused by the subsampling due to the hardware per-block computation of derivatives; horizontal derivatives have full vertical and half horizontal resolution, vertical derivatives have full horizontal and half vertical resolution.

这些 反褶假影 是由于硬件的每块计算导数而导致的二次采样引起的。水平导数具有全垂直和一半水平分辨率，垂直导数具有全水平和一半垂直分辨率。